Funktionsgraphen: graph
Attribute der graph Struktur
Die graph Struktur besitzt folgende Attribute:
| Attribut | Beschreibung | Default |
|---|---|---|
function |
Funktionsterm, z.B. sin(x) | |
label |
Label der Funktion in der Legende | wenn nicht angegeben: function |
plot_args |
Einstellungen zur Darstellung des Graphen | |
condition |
Bedingung. Siehe Beschreibung unten | |
max_y |
Werte größer als max_x werden als unendlich angesehen und nicht gezeichnet. |
100 |
min_y |
Werte kleiner als min_x werden als unendlich angesehen und nicht gezeichnet. |
-100 |
discontinuities |
Liste von Unstetigkeitsstellen, s.u. | [] |
Weitere Einstellungen: plot_args
Im Abschnitt plot_args kann man das Aussehen des Funktionsgraphen sehr detailliert einstellen. Die vollständige Liste der Parameter ist in der matplotlib Dokumentation zu finden.
Definitionslücken und Unstetigkeitsstellen
Unstetigkeitsstellen werden durch folgende Struktur beschrieben:
| Attribut | Beschreibung | Default |
|---|---|---|
x0 |
Stelle (x-Wert) der Unstetigkeit | |
belongs_to |
Welchen Wert nimmt die Funktion an der Sprungstelle an? Mögliche Angaben sind x>x0 (Funktion rechts von der Sprungstelle), x<x0 (Funktion links von der Sprungstelle), none (Definitionslücke). Diese Werte müssen genau so angegeben werden. |
Eine Definitionslücke kann auch in einer eigentlich stetigen Funktion gezeichnet werden.
Funktionsterme
Aus technischer Sicht sind Funktionsterme Python-Ausdrücke (expressions), in
denen die Variable x verwendet wird.
Neben den normalen Rechenoperationen (+, -, *, /) gibt es auch die Exponentiation (**).
Daneben stehen eine Reihe von Funktionen zur Verfügung, die sog.
ufunc-Funktionen aus dem numpy Pakte. Eine vollständige Liste ist in der
NuPy-Dokumentation
zu finden.
Praktisch bedeutet das, dass folgende Ausdrücke gültig sind:
x: f(x) = x, eine Gerade durch den Ursprung mit Steigung 1.2*x+1: Gerade mit Steigung 2, die die y-Achse bei (0,1) schneidet.sin(x),2*sin(x),sin(2*x),cos(x), ...x**2: f(x) = x².maximum(sin(x), sin(2*x)): sin(x) or sin(2*x), depending on which is greater.heaviside(x-2,0) * sin(x) + heaviside(2-x,1) * cos(x): sin(x) if x > 2, cos(x) if x <= 2.
Beispiel 1
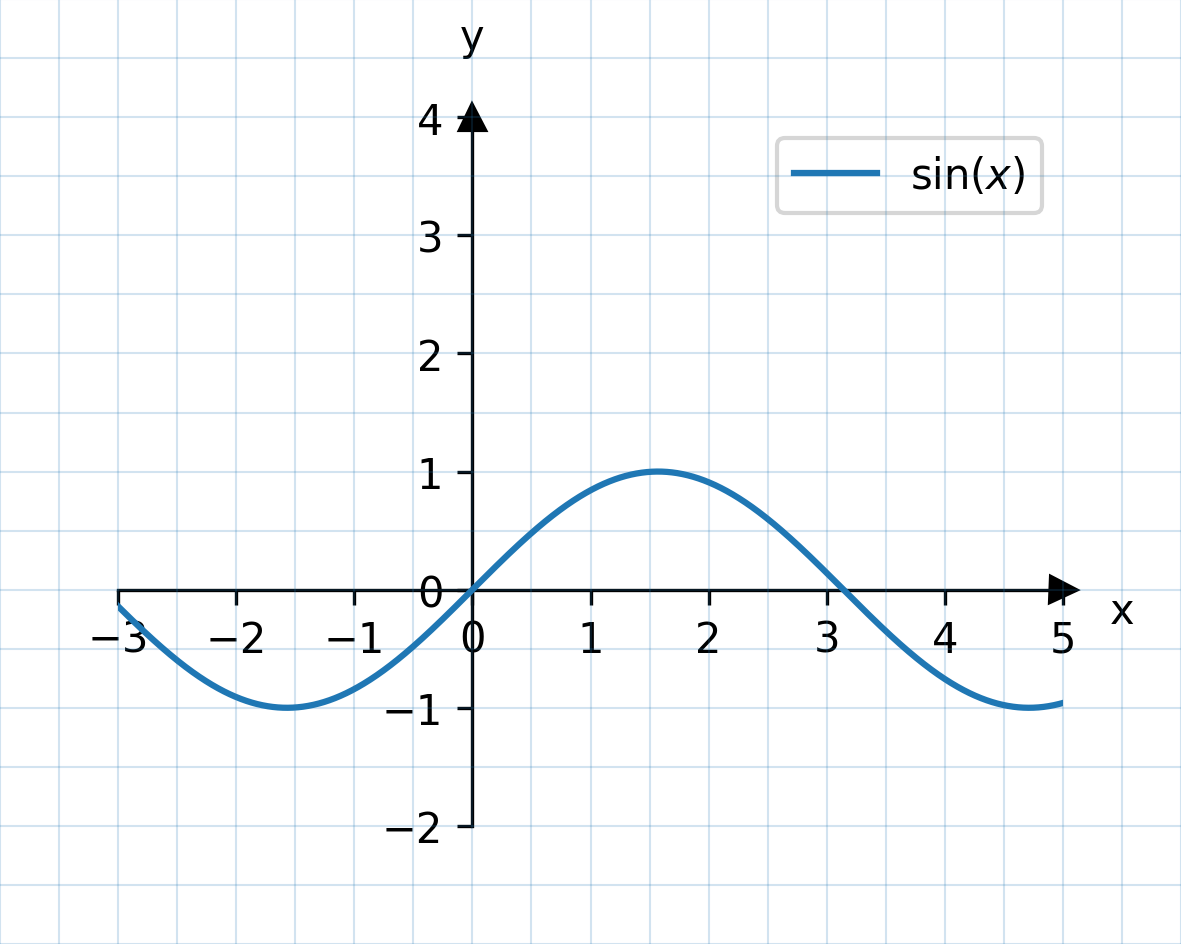
figure:
height: 8cm
width: 10cm
axes_descriptors:
- axes:
height: 6cm
width: 8cm
x_min: -3
y_min: -2
bottom: 1cm
left: 1cm
items:
- type: Graph
function: sin(x)
label: $\sin(x)$
Bedingungen (condition)
Das Attribut condition legt fest, welche Punkte des Graphen gezeichnet werden
sollen. Ähnlich zum Funktionsterm handelt es sich dabei um einen
Python-Ausdruck, in dem die Variablen x und y für die jeweiligen x- und
y-Werte verwendet werden können.
Es stehen die Vergleichs-Operatoren <, >, <=, >=, == (gleich), !=
(ungleich) zur Verfügung. Einzelne Vergleiche können mit and (und), or (oder)
sowie mit xor (exklusiv oder) verknüpft werden.
Es werden alle Punkte gezeichnet, für die die angegebene Bedingung erfüllt ist.
Beispiele für condition:
x > 0: x > 0x<2 or x>3: x < 2 oder x > 3y>0: alles rechts von der y-Achsey<x: alle Punkte unterhalb der Geraden y=x
Beispiel 2:
In diesem Beispiel wird die Bedingung -2 < x and x < 4 and y < 0.5 gesetzt, d.h. der Graph wird an den x-Stellen zwischen -2 und 4 gezeichnet, sofern der Funktionswert y kleiner als 0.5 ist.
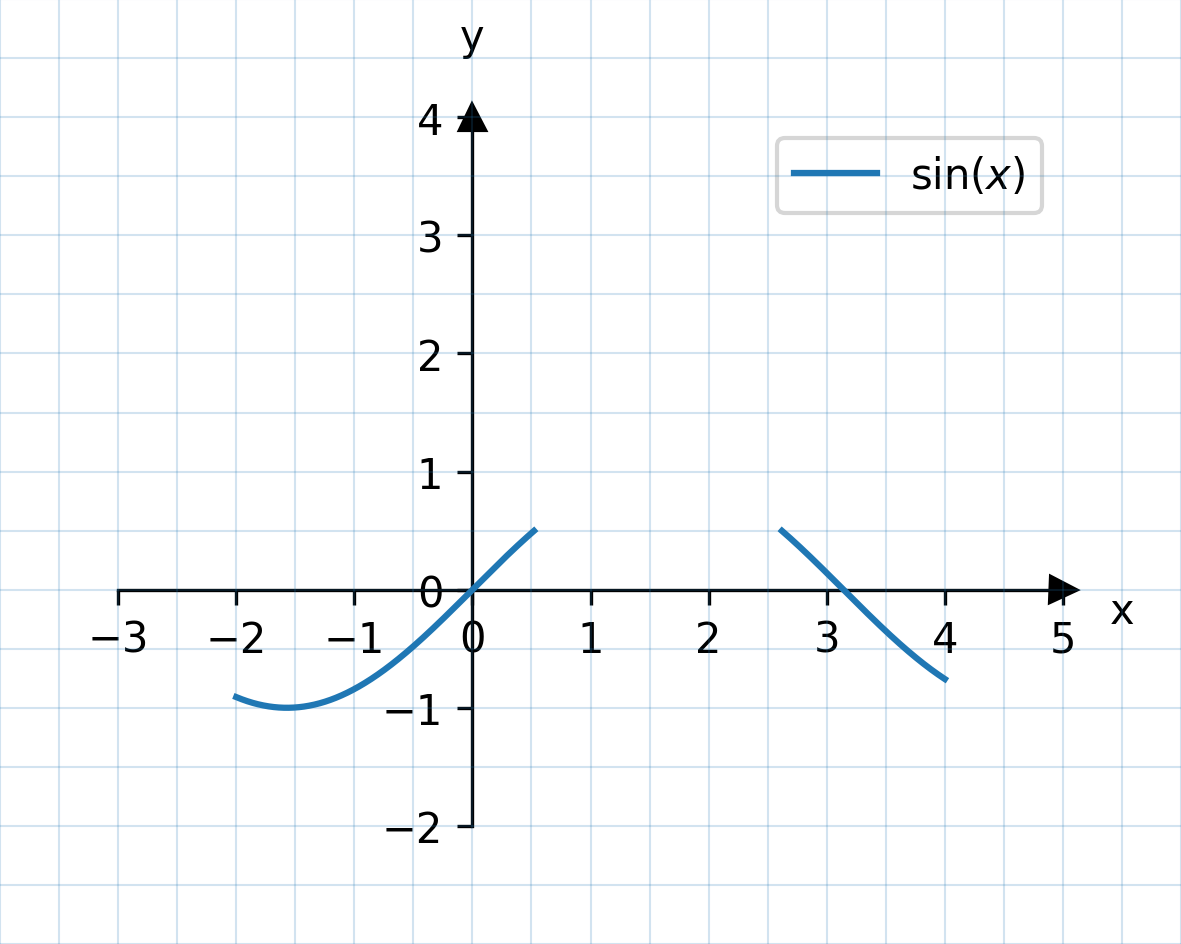
- Hier wird die Bedingung definiert.
Weitere Beispiele
Beispiel 3: Unstetigkeitsstellen
Dieses Beispiel zeigt die Verwendung von Unstetigkeitsstellen, am Beispiel der Stufenfunktion (heaviside). Es wird drei mal die selbe Funktion gezeichnet, wobei die Unstetigkeitsstelle mit dem jeweils angegebenen Wert für das Attribut belongs_to konfiguriert wurde.
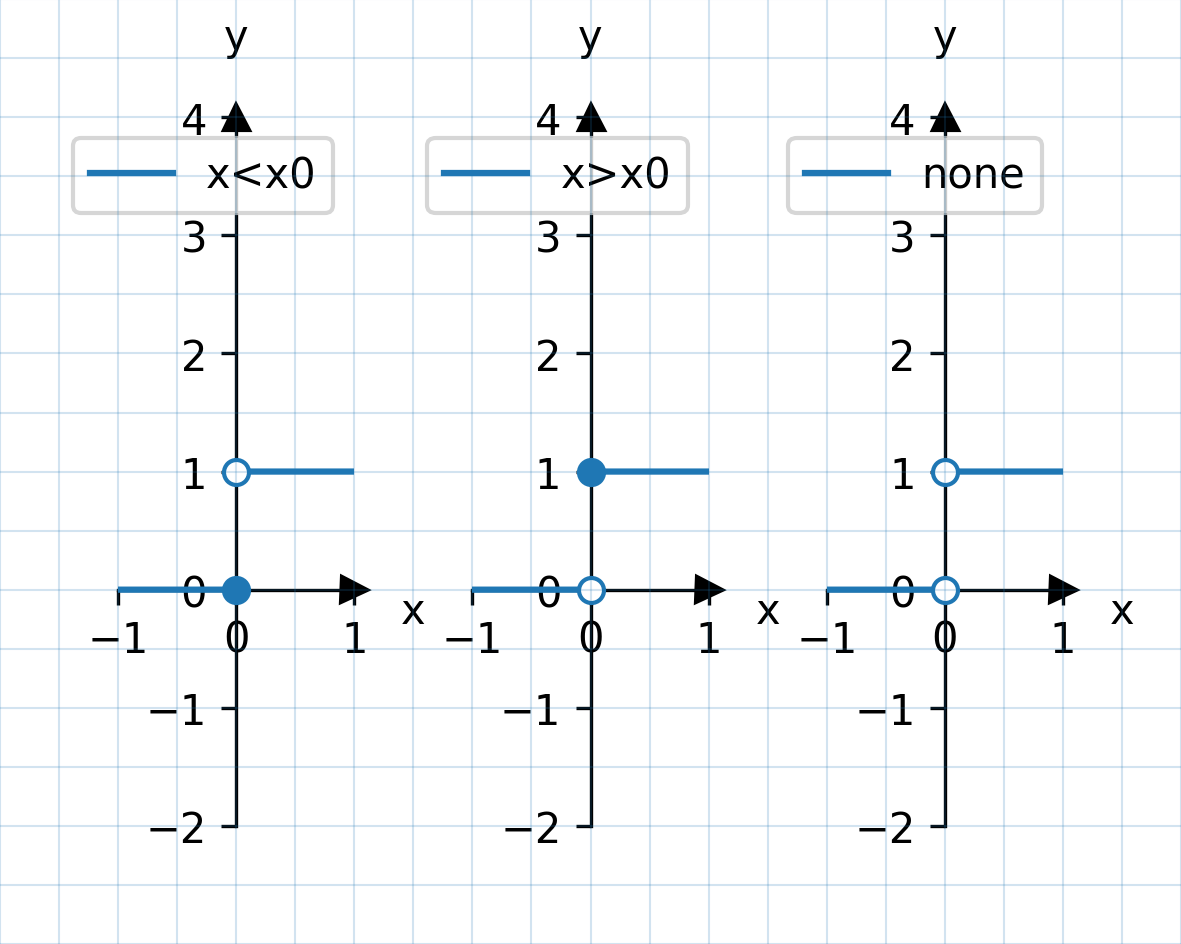
...
- axes:
height: 6cm
width: 2cm
x_min: -1
y_min: -2
bottom: 1cm
left: 1cm
items:
- type: Graph
function: heaviside(x,0)
discontinuities:
- x0: 0
belongs_to: x<x0
...
Beispiel 4: maximum und heavyside
Dieses Beispiel zeigt die Funktionen maximum und heavyside.
Die Funktion maximum(f1(x), f2(x)) liefert für jedes x den größeren der Werte
f1(x) und f2(x) zurück. Entsprechendes gilt für die minimum Funktion.
Praktisch bedeutet das, dass so der jeweils weiter oben liegende Graph zweier Funktionen gezeichnet wird -- zu sehen im linken Achsensystem unten.
Die heavyside Funktion ist auch als Stufenfunktion bekannt und eignet sich dazu, abschnittsweise definierte Funktionen zu definieren.
Allgemein kann man eine Funktion
schreiben als \(f(x) = \mathrm{heavyside}((x-x_0), 0) \cdot f_1(x) + \mathrm{heavyside}((x_0-x), 0) \cdot f_2(x)\). Beachte, dass das zweite Argument der heavyside-Funktion praktisch irrelevant ist, wenn man nur die Funktion plotten will.
Der rechte Graph setzt explizit die Unstetigkeitsstelle x=-1. In der Beschreibungsdatei sieht das so aus:
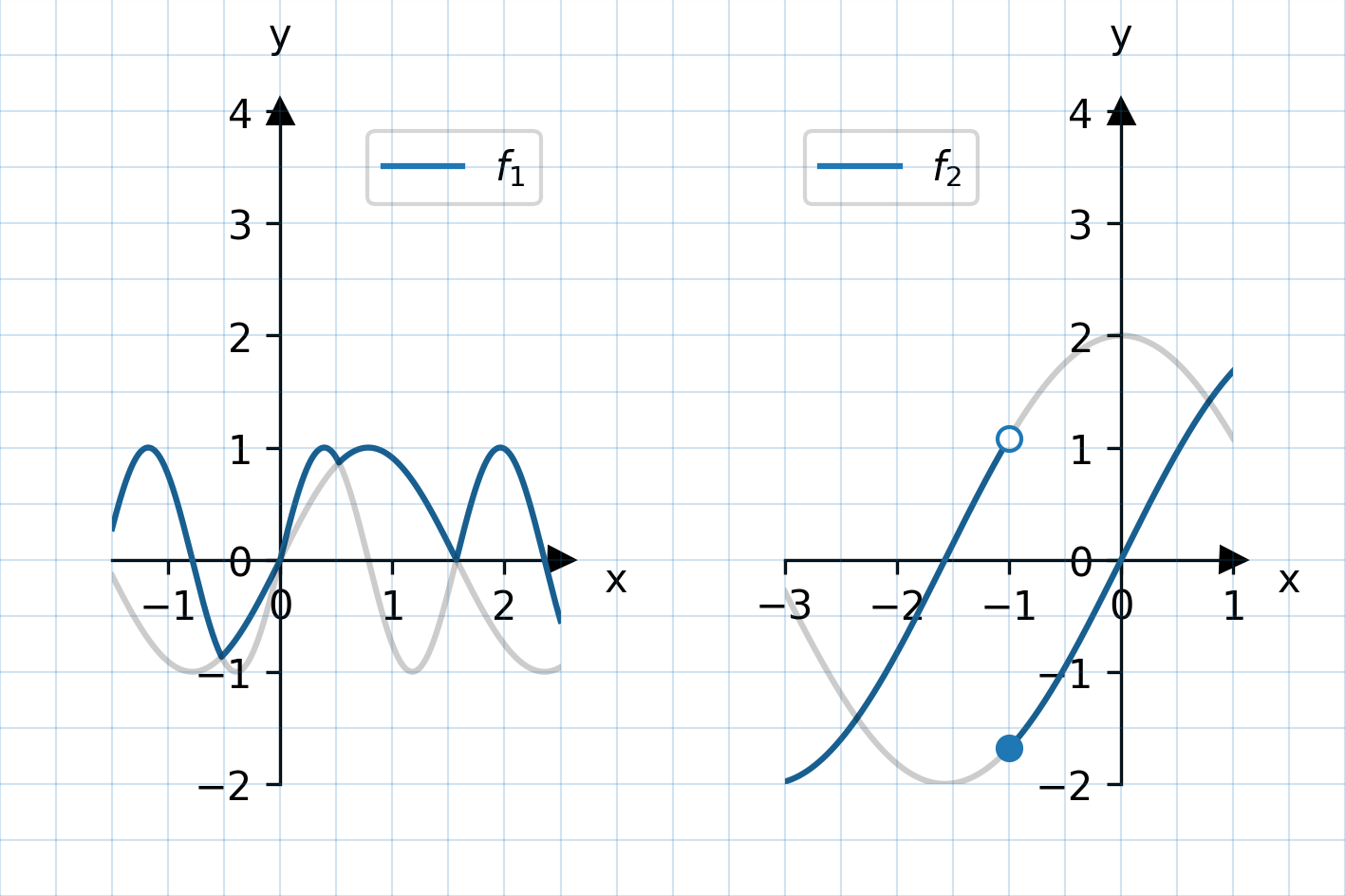
In jedem der beiden Achsensysteme zeigt jeweils der erste Graph das interessante Verhalten. Die anderen Graphen sind nur gezeichnet, um den weiteren Verlauf der zugrundeliegenden Graphen anzudeuten.
figure:
height: 8cm
width: 12cm
axes_descriptors:
- axes:
height: 6cm
width: 4cm
x_min: -1.5
y_min: -2
show_legend: true
bottom: 1cm
left: 1cm
items:
# Das ist der interessante Graph
- type: Graph
function: maximum(sin(4*x), sin(2*x))
label: $f_1$
- type: Graph
function: sin(4*x)
plot_args:
color: black
alpha: 0.2
label:
- type: Graph
function: sin(2*x)
plot_args:
color: black
alpha: 0.2
- axes:
height: 6cm
width: 4cm
x_min: -3
y_min: -2
legend_options:
loc: upper left
bottom: 1cm
left: 7cm
items:
# Das ist der interessante Graph
- type: Graph
function: heaviside(x+1,0) * 2*sin(x) + heaviside(-1-x,1) * 2*cos(x)
label: $f_2$
discontinuities:
- x0: -1
belongs_to: x>x0
- type: Graph
function: 2*sin(x)
plot_args:
color: black
alpha: 0.2
- type: Graph
function: 2*cos(x)
plot_args:
color: black
alpha: 0.2